Effect Size e a desigualdade de renda entre gêneros em Vitória

Ainda há um bocado de coisas para cobrir nessa série de “inferência 101” e para continuar os estudos trouxe a base da RAIS (Relação Anual de Informações Sociais) de 20171. Com ela, vamos introduzir o conceito de effect size e de quebra analisar a desigualdade de gênero em nossa querida capital Vitória.
OS DADOS
Coloco aqui duas opções para buscar esses dados:
- Manualmente, navegando em ftp://ftp.mtps.gov.br/pdet/microdados/RAIS/2017/ES2017.7z
- De forma programática via Python.
Escolhi o Python aqui porque não conheço um pacote no CRAN2 que lide com compressão 7zip — se souber, por favor, indique nos comentários! Se escolher baixar e descompactar via script, podemos executar códigos Python através do R com o {reticulate}:
1# ativando python
2library(reticulate)
3
4# escolhendo o ambiente
5use_condaenv("base")Depois de ativar o ambiente Python, vamos baixar e descompactar a base de dados para uma pasta chamada data dentro do diretório do nosso projeto. Se você baixou manualmente, crie a pasta data e cole o arquivo lá.
1# importando módulos
2import urllib.request as rq
3import py7zr
4
5# baixando dados
6url = "ftp://ftp.mtps.gov.br/pdet/microdados/RAIS/2017/ES2017.7z"
7rq.urlretrieve(url, "data/rais.7z")
8
9# descompactando
10rais = py7zr.SevenZipFile("data/rais.7z", mode="r")
11rais.extractall(path="data/")
12rais.close()Vamos precisar também da tabela do Código Brasileiro de Ocupações para entendermos as profissões das pessoas analisadas. Depois de fazer o download, coloque na pasta data junto com o arquivo da Rais.
Com os dados baixados, vamos importá-los, conhecê-los e começar a extrair sentido deles.
1# pacotes
2library(tidyverse)
3
4# importando a Rais
5# como os dados possuem caracteres especiais (acentos),
6# é necessário alterar o encoding para LATIN1
7data = read_delim("data/ES2017.txt", delim = ";",
8 locale = readr::locale(encoding = "LATIN1"),
9 col_names = FALSE,
10 skip = 1)
11
12# escolhendo as variáveis de interesse e renomeando colunas
13# também vamos precisar substituir vírgulas por pontos
14# se preferir, realize essa etapa via encoding
15data = data %>%
16 select(X8, X20, X26, X31, X35, X38) %>%
17 rename("cod_profissao" = X8,
18 "idade" = X20,
19 "municipio" = X26,
20 "cod_raca" = X31,
21 "rem_media" = X35,
22 "sexo" = X38) %>%
23 mutate(rem_media = as.numeric(str_replace_all(rem_media, ",", ".")),
24 sexo = as.integer(sexo),
25 idade = as.integer(idade))
26
27# importando tabela CBO
28cbo = read_delim("data/CBO2002.csv", delim = ";",
29 locale = readr::locale(encoding = "LATIN1"),
30 col_names = c("cod_profissao", "profissao"),
31 col_types = c("d", "c"),
32 skip = 1)
33
34# juntando ambas tabelas e filtrando apenas Vitória
35data = data %>%
36 inner_join(cbo, by = "cod_profissao") %>%
37 filter(municipio == 320530)Nossos dados agora têm essa cara:
1# visualizando dataframe
2head(data)## # A tibble: 6 x 7
## cod_profissao idade municipio cod_raca rem_media sexo profissao
## <dbl> <int> <dbl> <chr> <dbl> <int> <chr>
## 1 717020 42 320530 04 909. 1 Servente de obras
## 2 715210 28 320530 02 1167. 1 Pedreiro
## 3 717020 63 320530 02 1022. 1 Servente de obras
## 4 717020 59 320530 02 880. 1 Servente de obras
## 5 517410 29 320530 08 1880. 1 Porteiro de edifícios
## 6 715115 61 320530 08 0 1 Operador de escavadeiraDIFERENÇAS NO AGREGADO
Primeiramente, vamos tentar entender o que temos em mãos em termos de amostra:
1# quantidade de homens e mulheres
2data %>%
3 ggplot(aes(x = factor(sexo),
4 fill = factor(sexo),
5 label = scales::number(..count..))) +
6 geom_bar() +
7 geom_label(stat = "count",
8 show.legend = FALSE,
9 color = "grey30") +
10 scale_y_continuous(labels = scales::number) +
11 scale_fill_manual(name = "sexo",
12 labels = c("homens", "mulheres"),
13 values = c("lightblue", "salmon")) +
14 labs(x = "",
15 y = "quantidade",
16 title = "QUANTIDADE DE HOMENS E MULHERES",
17 subtitle = "amostra da cidade de Vitória-ES",
18 caption = "fonte: Rais/2017") +
19 theme_minimal() +
20 theme(text = element_text(family = "Century Gothic",
21 color = "grey30"),
22 axis.text.x = element_blank())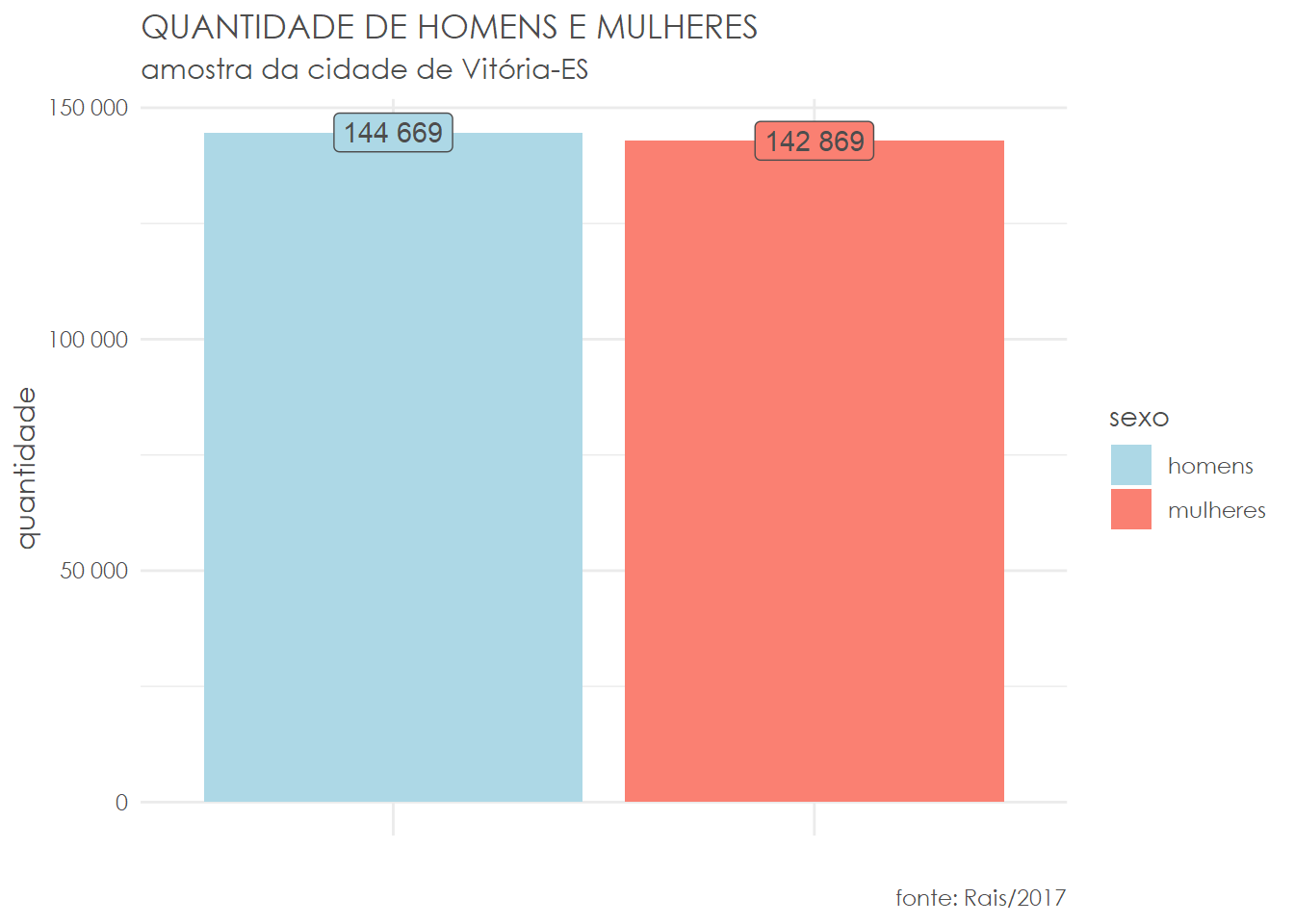
Temos praticamente a mesma quantidade de homens e mulheres em nossa amostra. Podemos, antes de realizar qualquer outra análise e aplicar quaisquer filtros, calcular a remuneração média:
1# remuneração média
2aggregate(data = data, rem_media ~ sexo, FUN = mean)## sexo rem_media
## 1 1 3925.187
## 2 2 2846.727No agregado, a renda média dos homens em Vitória é quase 40% maior que a das mulheres e mesmo quando consideramos a mediana ainda é quase 30% maior. Podemos verificar se essa diferença é significativa com um teste t, mas antes devemos verificar se seus pré-requisitos são atendidos.
1# quartis
2boxplot_data = data %>%
3 group_by(sexo) %>%
4 summarise(stats = list(fivenum(rem_media))) %>%
5 unnest(cols = c(stats))
6
7# boxplot
8data %>%
9 ggplot(aes(
10 x = factor(sexo),
11 y = rem_media,
12 fill = factor(sexo)
13 )) +
14 geom_boxplot() +
15 geom_label(
16 data = boxplot_data,
17 aes(x = factor(sexo), y = stats, label = scales::number(stats)),
18 nudge_x = 0.25,
19 show.legend = FALSE
20 ) +
21 coord_cartesian(ylim = c(0, 5000)) +
22 scale_y_continuous(labels = scales::number) +
23 scale_fill_manual(
24 name = "sexo",
25 labels = c("homens", "mulheres"),
26 values = c("lightblue", "salmon")
27 ) +
28 labs(
29 x = "",
30 y = "remuneração média",
31 title = "DISTRIBUIÇÃO DA REMUNERAÇÃO MÉDIA ENTRE HOMENS E MULHERES",
32 subtitle = "amostra da cidade de Vitória-ES",
33 caption = "fonte: Rais/2017"
34 ) +
35 theme_minimal() +
36 theme(
37 text = element_text(
38 family = "Century Gothic",
39 color = "grey30"
40 ),
41 axis.text.x = element_blank()
42 )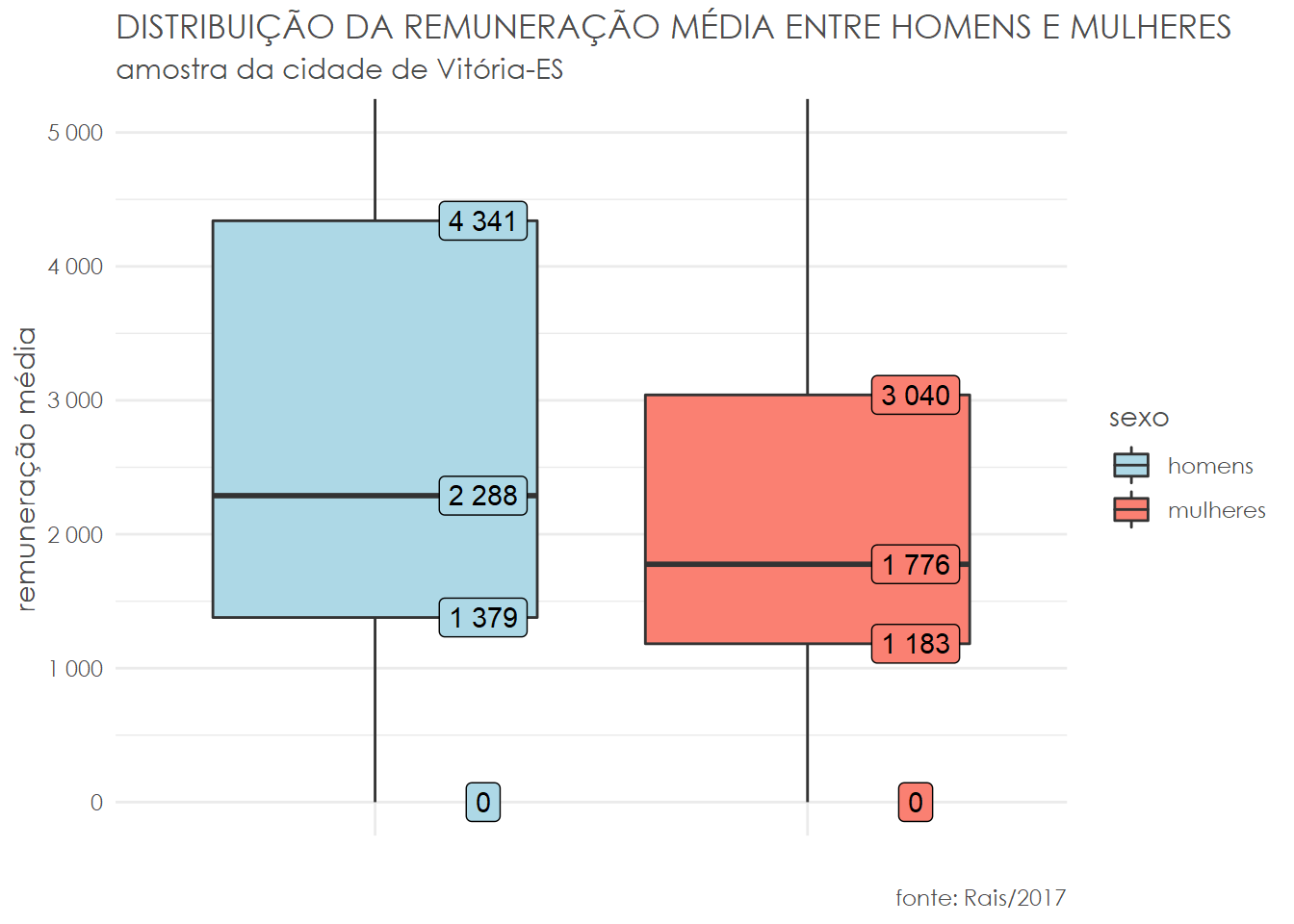
VERIFICANDO A HIPÓTESE DA NORMALIDADE
Sabemos que o teste t é um teste paramétrico e já discutimos anteriormente que, quando os dados não seguem uma distribuição próxima da normal, precisamos realizar transformações para alcançar a normalidade.
Você pode pensar que, com uma amostra desse tamanho, o Teorema Central do Limite garante a hipótese da normalidade. Entretanto, principalmente em dados com muitos outliers extremos, o tamanho da amostra necessária para convergência pode ser absurda, invalidando, na prática, a afirmação a partir da TCL.3. Portanto, defendo que devemos, sim, ter cuidado com essa hipótese mesmo lidando com grandes amostras.
A primeira análise nesse sentido é a visual. Podemos verificar que a distribuição apresenta fat tail e passa longe de uma normal, tanto pelo histograma quanto pelo Q-Q plot.
1# histograma
2data %>%
3 ggplot(aes(
4 x = rem_media,
5 fill = factor(sexo)
6 )) +
7 geom_histogram(binwidth = 500) +
8 coord_cartesian(xlim = c(0, 20000)) +
9 scale_y_continuous(labels = scales::number) +
10 scale_x_continuous(labels = scales::number) +
11 scale_fill_manual(
12 name = "sexo",
13 labels = c("homens", "mulheres"),
14 values = c("lightblue", "salmon")
15 ) +
16 labs(
17 x = "remuneração média",
18 y = "quantidade",
19 title = "DISTRIBUIÇÃO DA REMUNERAÇÃO MÉDIA ENTRE HOMENS E MULHERES",
20 subtitle = "amostra da cidade de Vitória-ES",
21 caption = "fonte: Rais/2017"
22 ) +
23 theme_minimal() +
24 theme(text = element_text(
25 family = "Century Gothic",
26 color = "grey30"
27 ))
28
29# qqplot
30# os dados estarão em cima da reta caso sejam distribuídos normalmente
31par(mfrow = c(1, 2))
32
33qqnorm(data[data$sexo == 1, ]$rem_media,
34 main = "Q-Q PLOT: HOMENS")
35qqline(data[data$sexo == 1, ]$rem_media)
36
37qqnorm(data[data$sexo == 2, ]$rem_media,
38 main = "Q-Q PLOT: MULHERES")
39qqline(data[data$sexo == 2, ]$rem_media)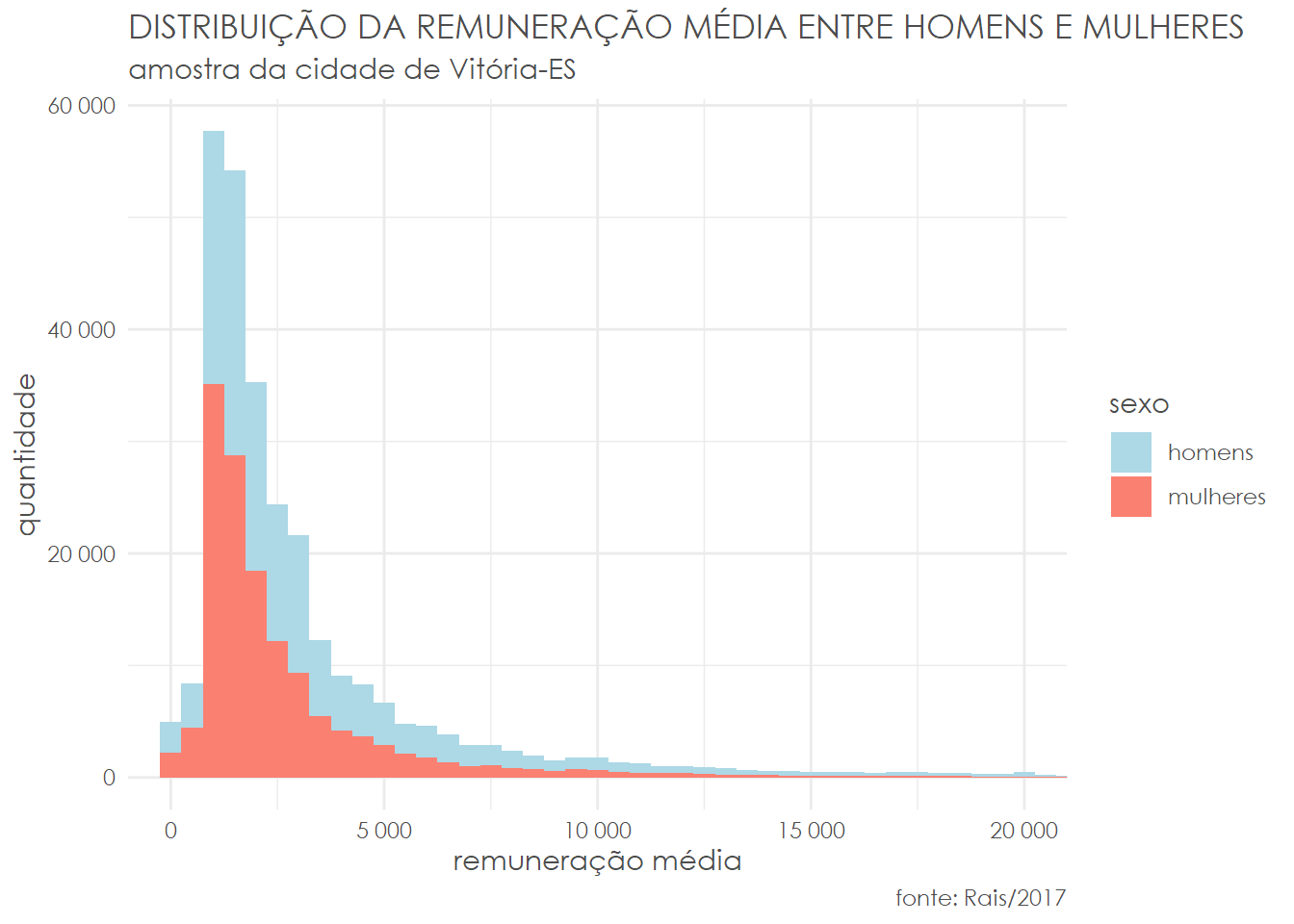
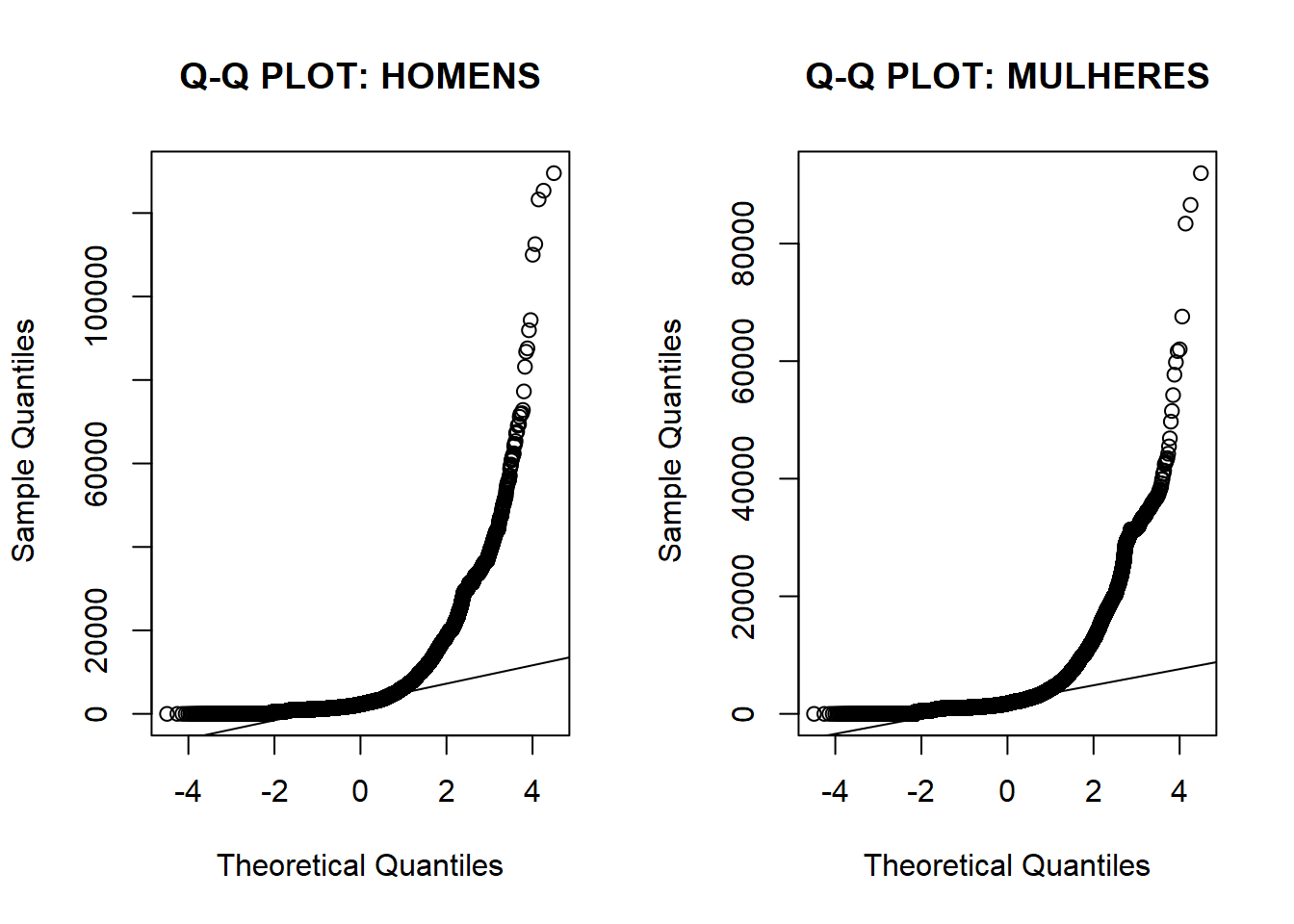
Podemos realizar um experimento para verificar a velocidade de convergência para a distribuição normal. Calculando a distribuição de mil médias de 30 homens cada, se ela apresentar distribuição próxima da normal poderemos assumir a normalidade e prosseguir com o trabalho. Caso contrário, precisaremos tratar a base.
1# garantir reprodutibilidade
2set.seed(1)
3
4# quantidade de amostras
5n = 1000
6
7# médias
8medias = rep(NA, n)
9
10# tirando amostras e calculando as médias
11for (i in 1:n) {
12 medias[i] = mean(
13 sample(data[data$sexo == 1, ]$rem_media,
14 size = 30, replace = TRUE
15 )
16 )
17}
18
19# qqplot
20qqnorm(medias)
21qqline(medias)
22
23# visualização
24hist(medias,
25 main = "DISTRIBUIÇÃO DAS MÉDIAS AMOSTRAIS",
26 xlab = "médias",
27 sub = "seed = 1"
28)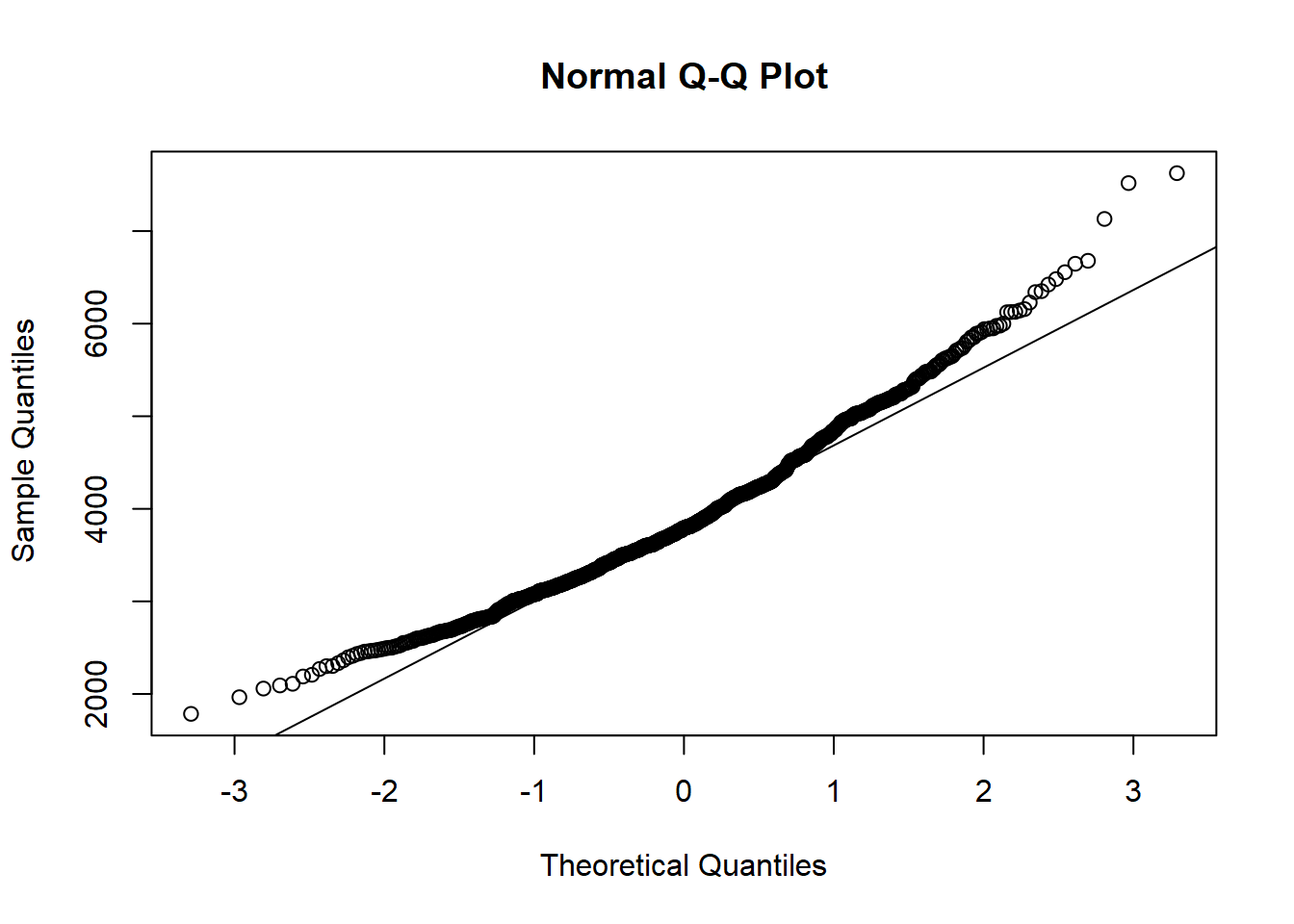
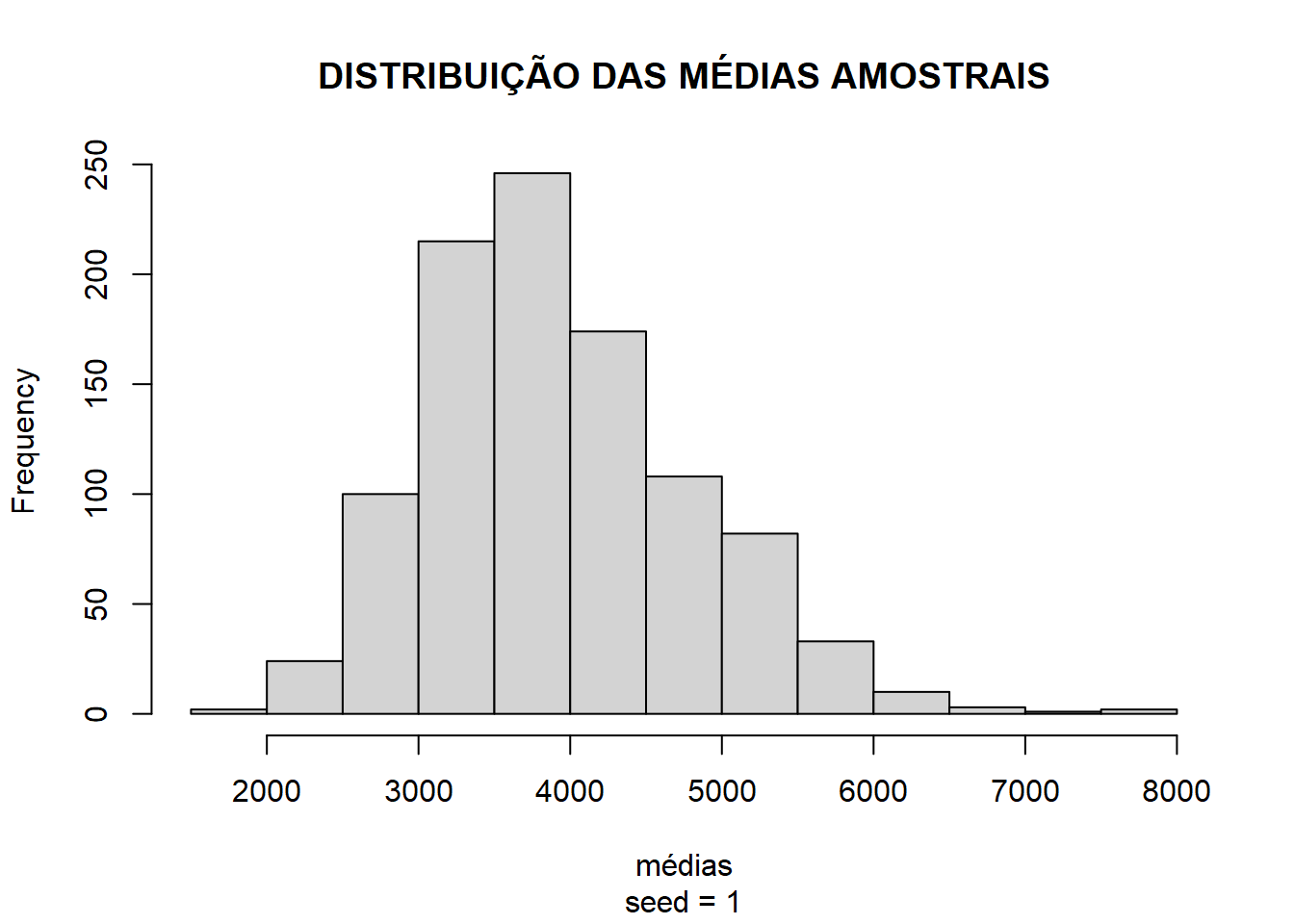
Ufa! O TCL se manteve em nossos dados e tanto o Q-Q plot quanto o histograma demonstraram distribuição próxima da normal, nos habilitando a prosseguir com os testes.
TESTE T
Agora que garantimos os pré-requisitos, vamos testar se a diferença entre as médias é significativa. Para isso, vamos usar o pacote {infer}:
1# transformando variável `sexo`
2data = data %>%
3 mutate(sexo = ifelse(sexo == 1, "homem", "mulher"))
4
5# carregando pacote
6library(infer)
7
8# calculando estatística t
9estatistica_calculada = data %>%
10 specify(rem_media ~ sexo) %>%
11 calculate(stat = "t", order = c("homem", "mulher"))
12
13# gerando distribuição nula
14distr_nula = data %>%
15 specify(rem_media ~ sexo) %>%
16 hypothesise(null = "independence") %>%
17 generate(reps = 100, type = "permute") %>%
18 calculate(stat = "t", order = c("homem", "mulher"))
19
20# visualizando distribuição nula e estatística do teste
21distr_nula %>%
22 visualize(method = "both") +
23 shade_p_value(estatistica_calculada, direction = "greater")
24
25# calculando p-valor
26distr_nula %>%
27 get_p_value(obs_stat = estatistica_calculada, direction = "greater")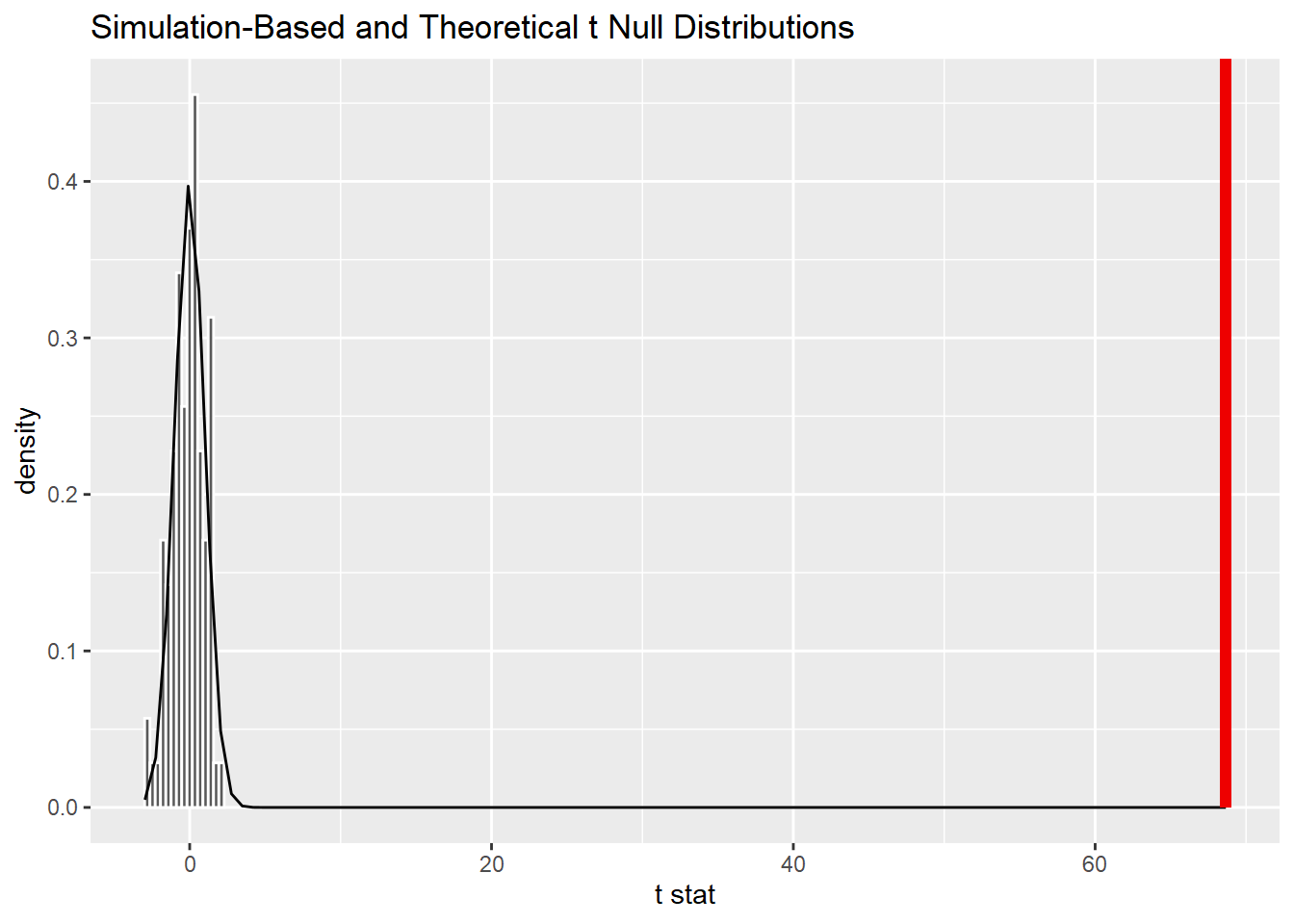
## # A tibble: 1 x 1
## p_value
## <dbl>
## 1 0Com p-valor de 0% e uma estatística calculada a quilômetros da distribuição nula, fica bem claro que a diferença é significativa. Entretanto, isso não quer dizer que ela seja grande ou pequena. É aí que entram os indicadores de tamanho de efeito.
TAMANHO DO EFEITO: Cohen’s D
Nesse post eu mostrei que o tamanho da amostra é determinante para o teste t e tenderemos a rejeitar a hipótese nula quanto maior for a amostra. Aqui, se tratando de mais de 140 mil observações para cada sexo, dificilmente essas diferenças não seriam significativas. Para complementar esse teste, podemos calcular o tamanho do efeito com a estatística d de Cohen.
Muito usada no campo da saúde em experimentos com testes t pareados, quando é preciso definir o efeito de uma ação em um grupo de tratamento em relação ao grupo de controle, a estatística d de Cohen é um indicador de diferenças padronizadas e é particularmente valiosa para quantificar o efeito de uma intervenção, seja em políticas públicas ou em ações de marketing na sua empresa. Isso quer dizer que ele enfatiza o tamanho da diferença entre as médias, sem confundir com a questão do tamanho da amostra.
Por ser padronizado (i.e. não é medido na unidade da amostra, aqui em BR$, mas sim em desvios-padrões) pode ser facilmente comparado à diferentes experimentos. Sua forma de cálculo é a seguinte: \[ d = \frac{\text{média do grupo experimental} - \text{média do grupo de controle}}{\text{desvio padrão agrupado}} \]
Para duas médias fixadas, quanto menor for o desvio padrão, maior será a estatística d. Por outro lado, quanto maior for o desvio padrão, menor será o tamanho do efeito.
No R, vamos utilizar o pacote {effectsize}:
1# carregando pacote
2library(effectsize)
3
4# calculando a diferença padronizada
5cohens_d(
6 data[data$sexo == "homem", ]$rem_media,
7 data[data$sexo == "mulher", ]$rem_media
8)
9
10# interpretando a estatística d
11interpret_d(0.26, "gignac2016")## Cohen's d | 95% CI
## ------------------------
## 0.26 | [0.28, 0.28]
##
## - Estimated using pooled SD.## [1] "small"
## (Rules: gignac2016)Com uma estatística \(d=0.26\), a diferença é considerada pequena. Na escala de Gignac & Szodorai (2016):
1rules(
2 c(0.2, 0.41, 0.63),
3 c("muito pequeno", "pequeno", "moderado", "grande"),
4 "Gignac & Szodorai (2016)"
5)## # Reference thresholds (Gignac & Szodorai (2016))
##
## muito pequeno <= 0.2 < pequeno <= 0.41 < moderado <= 0.63 < grandeEm uma situação de equidade, 50% das mulheres teriam remuneração abaixo do que o homem médio, enquanto a outra metade teria remuneração superior.
Um efeito de 0.26, equivale a dizer que 62% das mulheres teriam remuneração abaixo da remuneração do homem médio em Vitória, enquanto apenas 38% receberiam mais do que o homem médio4.
Claro que analisar o agregado significa olhar para a média. Como serão essas diferenças dentre as diversas profissões?
DIFERENÇAS ENTRE PROFISSÕES
Podemos estender nossa análise verificando em quais profissões há maior e menor divergência na remuneração.
1# criando dataframe de diferenças na remuneração
2# profissões selecionadas
3diferencas = data %>%
4 mutate(profissao = case_when(
5 str_detect(profissao, "Advogado") ~ "Advogados",
6 str_detect(profissao, "Engenheiro") ~ "Engenheiros",
7 str_detect(profissao, "Médico") ~ "Médicos",
8 str_detect(profissao, "Gerente") ~ "Gerentes",
9 str_detect(profissao, "Dirigentes|Diretor") ~ "Diretores",
10 str_detect(profissao, "Economista") ~ "Economistas",
11 str_detect(profissao, "Analista") ~ "Analistas",
12 str_detect(profissao, "Técnico") ~ "Técnicos",
13 str_detect(profissao, "Enfermeiro") ~ "Enfermeiros",
14 str_detect(profissao,
15 "(Professor)(.*)(ensino superior)(.*)") ~ "Prof. Ensino Superior",
16 TRUE ~ "Outros"
17 )) %>%
18 group_by(sexo, profissao) %>%
19 summarise(
20 renda = mean(rem_media),
21 n = n()
22 ) %>%
23 ungroup() %>%
24 pivot_wider(names_from = sexo, values_from = c(renda, n)) %>%
25 mutate(dif = renda_homem - renda_mulher) %>%
26 arrange(desc(dif))
27
28# visualizando tabela
29diferencas## # A tibble: 11 x 6
## profissao renda_homem renda_mulher n_homem n_mulher dif
## <chr> <dbl> <dbl> <int> <int> <dbl>
## 1 Diretores 13559. 6994. 393 228 6565.
## 2 Engenheiros 13997. 10446. 1850 409 3550.
## 3 Advogados 8625. 5658. 244 342 2966.
## 4 Economistas 8251. 5576. 168 184 2675.
## 5 Gerentes 6599. 4463. 3659 3477 2136.
## 6 Técnicos 4790. 2731. 10434 10493 2060.
## 7 Analistas 5647. 4039. 2931 1869 1607.
## 8 Prof. Ensino Superior 7384. 6470. 1248 1062 914.
## 9 Outros 3427. 2606. 121362 120682 820.
## 10 Médicos 8232. 7704. 1840 1984 528.
## 11 Enfermeiros 4166. 4439. 540 2139 -273.Dentre as profissões selecionadas, apenas a de enfermagem tem remuneração média maior para as mulheres. Os homens levam vantagem em todos os demais. Colocando em gráfico:
1# gráfico
2diferenca_media = 3925.18 - 2846.727
3setas = tibble(
4 x1 = c(2.9, 9.6, 8.3),
5 x2 = c(3.5, 9.2, 7.4),
6 y1 = c(2000, 6000, 0),
7 y2 = c(1200, 6300, -270)
8)
9
10diferencas %>%
11 ggplot(aes(x = reorder(profissao, desc(profissao)), y = dif)) +
12 geom_hline(yintercept = diferenca_media, color = "grey85") +
13 geom_segment(
14 aes(y = diferenca_media, yend = dif, xend = profissao),
15 color = "grey85", size = .7
16 ) +
17 geom_point(aes(size = renda_homem), color = "#F06337") +
18 scale_y_continuous(labels = scales::number) +
19 scale_size_continuous(labels = scales::number, range = c(1, 10)) +
20 annotate("text",
21 x = 2.5, y = 2000, size = 3.5, color = "grey85",
22 label = "a diferença média é de
23R$ 1.078"
24 ) +
25 annotate ("text",
26 x = 10.5, y = 5500, size = 3.5, color = "grey85",
27 label = paste("posições de executivo",
28 "é onde a diferença é maior",
29 "e é também onde estão
30os maiores salários",
31 sep = "
32"
33 )) +
34 annotate("text",
35 x = 9, y = 250, size = 3.5, color = "grey85",
36 label = paste(
37 "dentre essas profissões,",
38 "apenas as enfermeiras",
39 "recebem mais que homens",
40 sep = "
41"),
42 ) +
43 geom_curve(
44 data = setas, aes(x = x1, y = y1, xend = x2, yend = y2),
45 arrow = arrow(length = unit(0.1, "inch")),
46 size = 0.3, color = "grey85", curvature = 0.3
47 ) +
48 coord_flip() +
49 labs(
50 x = "",
51 y = "diferença salarial em R$",
52 size = "rem. média
53(homem)",
54 title = "desigualdade de gênero",
55 subtitle = paste("as disparidades salarias evidenciam o longo caminho na superação da colocação",
56 "da mulher como profissional de segunda categoria no mercado de trabalho",
57 sep = "
58"),
59 caption = "fonte: Rais 2017, Vitória/ES | elaboração: Alberson Miranda"
60 ) +
61 theme(
62 panel.grid = element_blank(),
63 plot.background = element_rect(fill = "#002538"),
64 panel.background = element_rect(fill = "#002538"),
65 text = element_text(
66 family = "Century Gothic",
67 color = "grey85"
68 ),
69 axis.text = element_text(color = "grey85", size = 10),
70 axis.ticks = element_line(color = "grey85"),
71 plot.title = element_text(size = 36, margin = margin(10, 0, 5, 10)),
72 plot.subtitle = element_text(
73 hjust = 0,
74 margin = margin(0, 0, 30, 0),
75 size = 16
76 ),
77 plot.caption = element_text(hjust = 1),
78 plot.title.position = "plot",
79 panel.border = element_rect(color = "grey85", fill = NA),
80 legend.background = element_rect(fill = "#002538"),
81 legend.key = element_rect(fill = "#002538")
82 )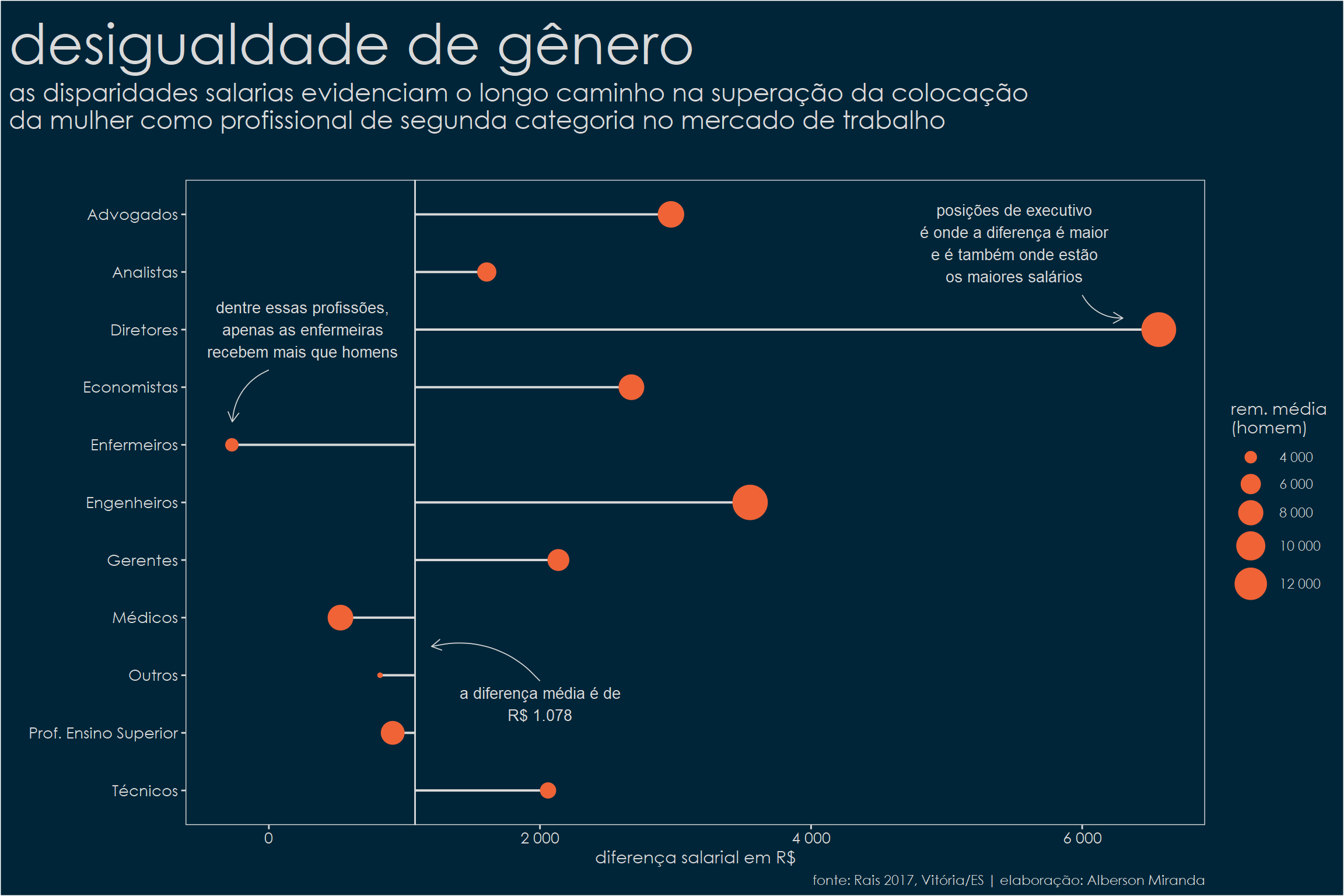
Dentre essas profissões que escolhemos, vamos analisar o tamanho do efeito para médicos e executivos (dirigentes e diretores).
DISPARIDADE SALARIAL ENTRE MÉDICOS
Primeiramente, vamos verificar a significância da diferença. Como esperado, ela é significativa.
1# calculando estatística t
2estatistica_calculada = data %>%
3 filter(str_detect(profissao, "Médico")) %>%
4 specify(rem_media ~ sexo) %>%
5 calculate(stat = "t", order = c("homem", "mulher"))
6
7# gerando distribuição nula
8distr_nula = data %>%
9 filter(str_detect(profissao, "Médico")) %>%
10 specify(rem_media ~ sexo) %>%
11 hypothesise(null = "independence") %>%
12 generate(reps = 100, type = "permute") %>%
13 calculate(stat = "t", order = c("homem", "mulher"))
14
15# calculando intervalo de confiança
16percentile_ci = get_ci(distr_nula)
17
18# visualizando distribuição nula e estatística do teste
19distr_nula %>%
20 visualize(method = "both") +
21 shade_p_value(estatistica_calculada, direction = "greater") +
22 shade_confidence_interval(endpoints = percentile_ci)
23
24# calculando p-valor
25distr_nula %>%
26 get_p_value(obs_stat = estatistica_calculada, direction = "greater")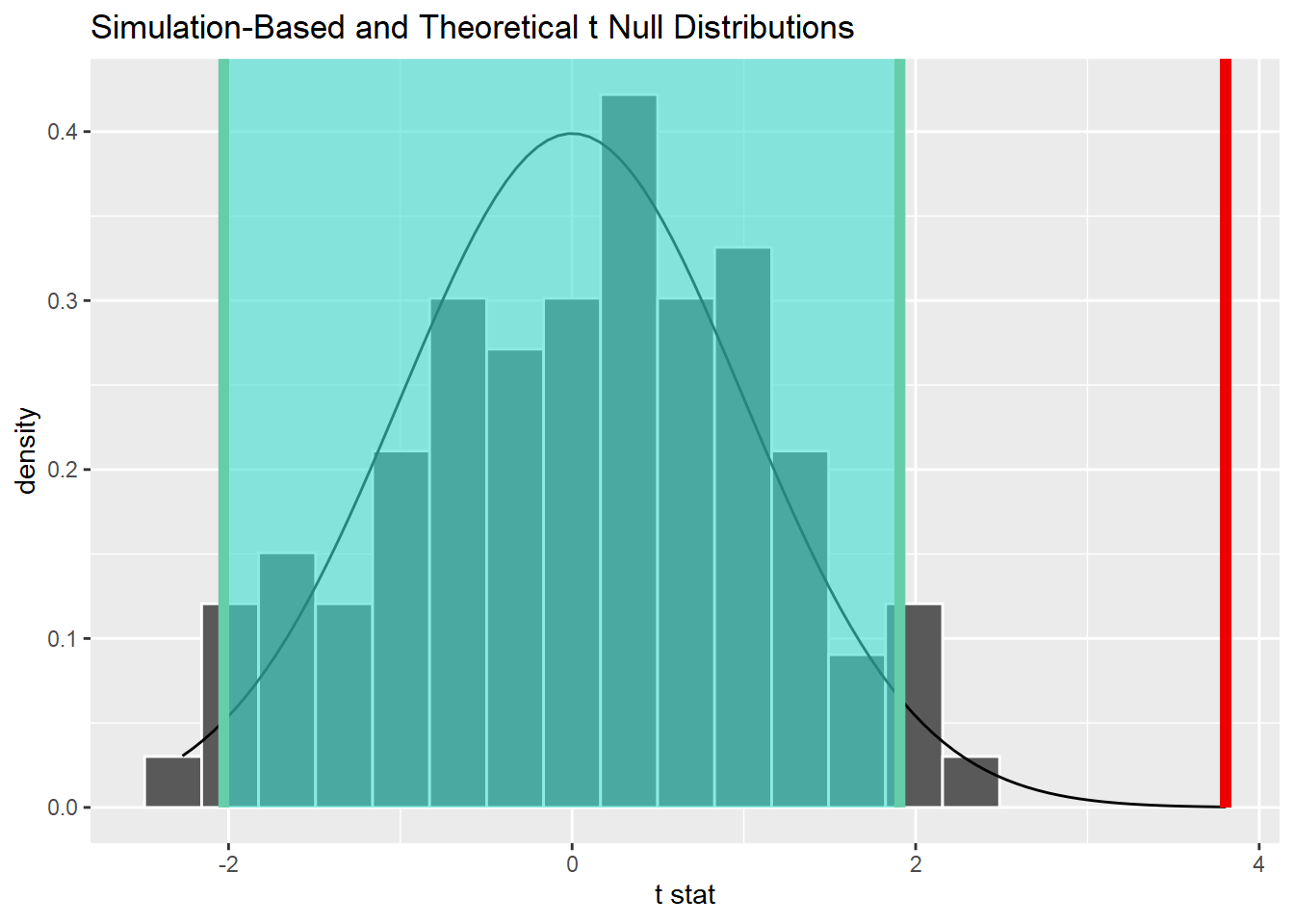
## # A tibble: 1 x 1
## p_value
## <dbl>
## 1 0Em seguida, vamos calcular o tamanho do efeito.
1 # calculando a diferença padronizada
2 cohens_d(
3 data[data$sexo == "homem" &
4 str_detect(data$profissao, "Médico"), ]$rem_media,
5 data[data$sexo == "mulher" &
6 str_detect(data$profissao, "Médico"), ]$rem_media
7 )
8
9 # interpretando a estatística d
10 interpret_d(0.12, "gignac2016")## Cohen's d | 95% CI
## ------------------------
## 0.12 | [0.06, 0.19]
##
## - Estimated using pooled SD.## [1] "very small"
## (Rules: gignac2016)Com uma estatística d de 0.12, temos um efeito muito pequeno na escala de Gignac & Szodorai (2016). Isso significa que 54% das médicas da cidade de Vitória teriam remuneração abaixo do que o médico médio do município, enqaunto 46% receberiam mais que o médico médio.
DISPARIDADE SALARIAL EM CARGOS EXECUTIVOS
Repetindo o mesmo procedimento para as pessoas em cargos executivos, vemos que a diferença também é significativa.
1# calculando estatística t
2estatistica_calculada = data %>%
3 filter(str_detect(profissao, "Dirigentes|Diretor")) %>%
4 specify(rem_media ~ sexo) %>%
5 calculate(stat = "t", order = c("homem", "mulher"))
6
7# gerando distribuição nula
8distr_nula <- data %>%
9 filter(str_detect(profissao, "Dirigentes|Diretor")) %>%
10 specify(rem_media ~ sexo) %>%
11 hypothesise(null = "independence") %>%
12 generate(reps = 100, type = "permute") %>%
13 calculate(stat = "t", order = c("homem", "mulher"))
14
15# calculando intervalo de confiança
16percentile_ci <- get_ci(distr_nula)
17
18# visualizando distribuição nula e estatística do teste
19distr_nula %>%
20 visualize(method = "both") +
21 shade_p_value(estatistica_calculada, direction = "greater") +
22 shade_confidence_interval(endpoints = percentile_ci)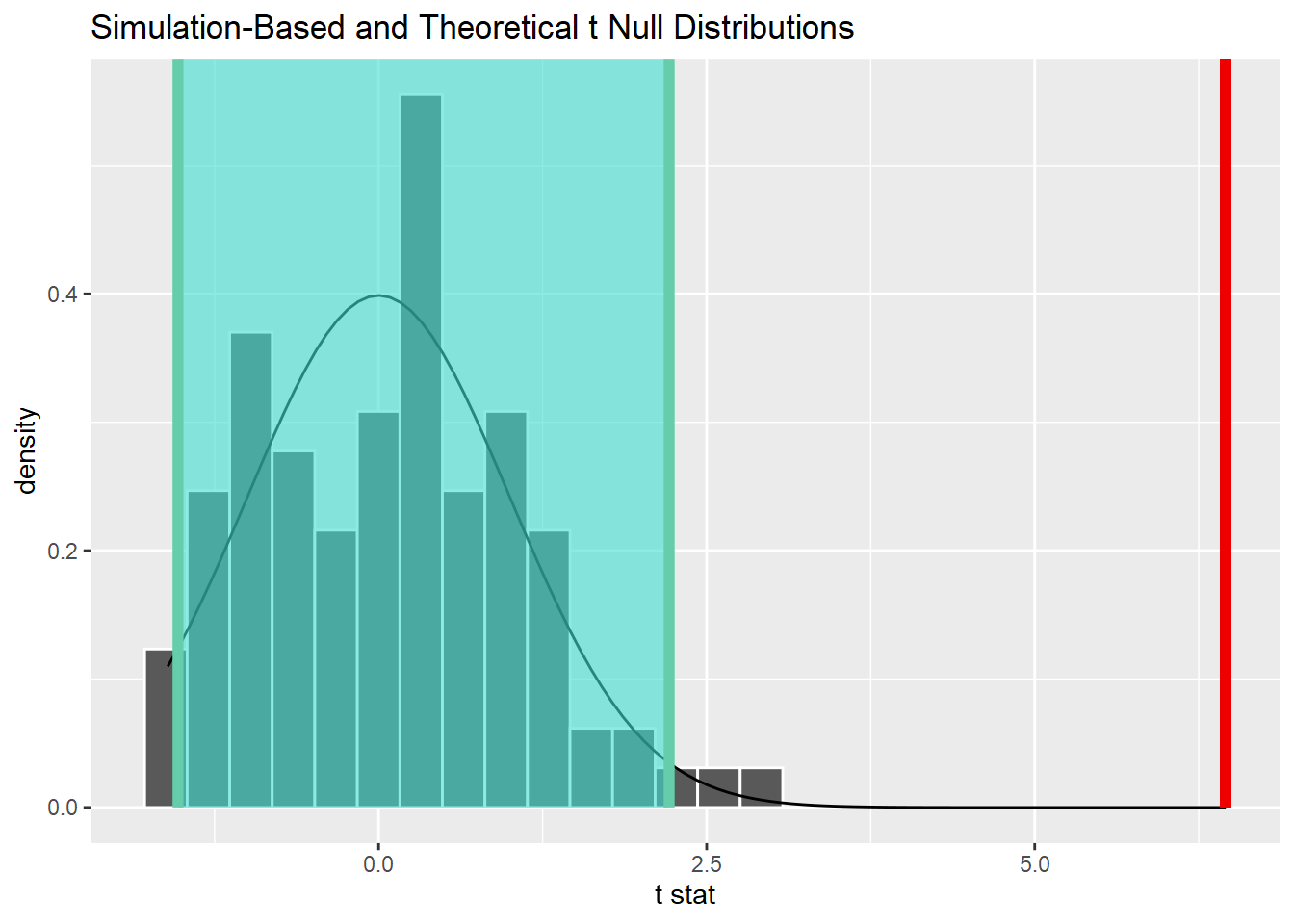
E calculando o tamanho do efeito:
1 # calculando a diferença padronizada
2 cohens_d(
3 data[data$sexo == "homem" &
4 str_detect(data$profissao, "Dirigentes|Diretor"), ]$rem_media,
5 data[data$sexo == "mulher" &
6 str_detect(data$profissao, "Dirigentes|Diretor"), ]$rem_media
7 )
8
9 # interpretando a estatística d
10 interpret_d(0.47, "gignac2016")
11 ## Cohen's d | 95% CI
## ------------------------
## 0.47 | [0.30, 0.63]
##
## - Estimated using pooled SD.## [1] "moderate"
## (Rules: gignac2016)Com uma estatística d de 0.47, temos um efeito moderado na escala de Gignac & Szodorai (2016). Isso significa dizer que 69% das mulheres em posição de dirigentes e diretoras receberiam menos do que o homem médio na mesma posição.
CONSIDERAÇÕES
A escala de Gignac & Szodorai é apenas uma rule of thumb dentre outras — além dela, duas regras muito usadas são as regras de Cohen (1988) e de Sawilowsky (2009). Pode ser que para a natureza desse problema a interpretação sugerida por essas regras não seja razoável. Nelas, uma estatística d de 0.47 é considerada pequena ou moderada. No entanto, se tratando de disparidades salariais entre gêneros, podemos argumentar que uma taxa de 69% das mulheres com remuneração menor que a do homem médio seja um resultado expressivo, justificando uma escala específica.
De qualquer forma, a desigualdade é escancarada e ainda há várias variáveis a serem exploradas nesse contexto — se adicionarmos raça, qual será o comportamento?
Se você chegou até aqui e tem sugestão de variáveis, escalas para interpretação ou outras profissões para analisarmos, deixe seu comentário que a gente atualiza com um edit!
Escolhi 2017 porque os dados mais atuais estão agrupados com Minas Gerais e Rio de Janeiro, ficando muito pesado para uma análise casual.↩︎
Compreehensive R Archive Network.↩︎
A tabela de interpretação de effect sizes pode ser consultada neste artigo.↩︎
Postagens nesta série
- Effect Size e a desigualdade de renda entre gêneros em Vitória
- Comparando variâncias: o teste F
- Chutou ou não chutou? O teste t para uma amostra
- Atestando diferenças em médias: o teste t para amostras independentes