Comparando variâncias: o teste F

Nov 20, 2020 · 6 min read · inferencia R ·

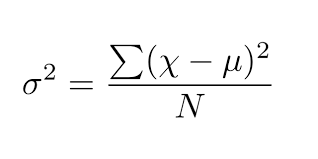
Antes de eu entrar no assunto machine learning, porque ~~é um buraco sem fundo~~ devo me demorar quando entrar, quero cobrir um pouco mais do básico em inferência.

Nesse post eu disse que para realizar o teste t em duas amostras independentes deveríamos saber antes se as variâncias dessas amostras são iguais ou diferentes. Vamos ver como atestar isso agora. A base utilizada será a german credit data.

1# importando dados
2# obs.: o -1 é para remover a primeira coluna, que é apenas o índice
3data = readr::read_csv("german_credit_data.csv")[-1]
4
5# visualizando
6print(data)

## # A tibble: 1,000 x 9
##      Age Sex      Job Housing `Saving account~ `Checking accoun~ `Credit amount`
##    <dbl> <chr>  <dbl> <chr>   <chr>            <chr>                       <dbl>
##  1    67 male       2 own     <NA>             little                       1169
##  2    22 female     2 own     little           moderate                     5951
##  3    49 male       1 own     little           <NA>                         2096
##  4    45 male       2 free    little           little                       7882
##  5    53 male       2 free    little           little                       4870
##  6    35 male       1 free    <NA>             <NA>                         9055
##  7    53 male       2 own     quite rich       <NA>                         2835
##  8    35 male       3 rent    little           moderate                     6948
##  9    61 male       1 own     rich             <NA>                         3059
## 10    28 male       3 own     little           moderate                     5234
## # ... with 990 more rows, and 2 more variables: Duration <dbl>, Purpose <chr>

Da mesma forma que o teste t, podemos testar se a medida de uma amostra é significativamente diferente de um valor escolhido ou podemos testar em relação à outra amostra — se maior, menor ou diferente. Para este exercício, vamos testar se a variância da variável Credit amount (limite de crédito) é o mesmo para homens e mulheres que vivem de aluguel. Primeiro, vamos calcular os desvios-padrão populacionais:

1# obtendo amostras
2homens = data[data$Sex == "male" & data$Housing == "rent",]$`Credit amount`
3mulheres = data[data$Sex == "female" & data$Housing == "rent",]$`Credit amount`
4
5# calculando desvio padrão
6sd(homens)
7sd(mulheres)

## [1] 2846.647

## [1] 2235.225

Verificamos que o limite de crédito dos homens tem um desvio-padrão de DM$ 2.846, enquanto o das mulheres é de DM$ 2235¹, o que quer dizer que o limite de crédito dos homens varia mais em torno da média do que das mulheres. O que gostaríamos de saber agora é se essa diferença é significativamente diferente. Vamos ao teste!

O TESTE

O teste F, dentre suas várias outras aplicações, é usado em conjunto com o teste t de duas amostras — quando é preciso conhecer se as duas populações amostradas têm a mesma variância ou não.

Ele também é um teste paramétrico, o que significa que ele supõe que as populações têm aproximadamente uma certa de distribuição, neste caso a normal. Portanto, temos de primeiramente garantir que essa hipótese seja atendida.

VERIFICANDO A HIPÓTESE DE NORMALIDADE

Primeiramente, vamos plotar as densidades para verificar se sua distribuição é plausível com a hipótese de normalidade:

 1# dados de densidade
 2d1 = density(homens)
 3d2 = density(mulheres)
 4
 5# separando o grid em 2 colunas
 6par(mfrow = c(1,2))
 7
 8# visualização
 9plot(d1,
10  main = "Density Plot: homens")
11polygon(d1, col = "lightblue")
12
13plot(d2,
14  main = "Density Plot: mulheres")
15polygon(d2, col = "salmon")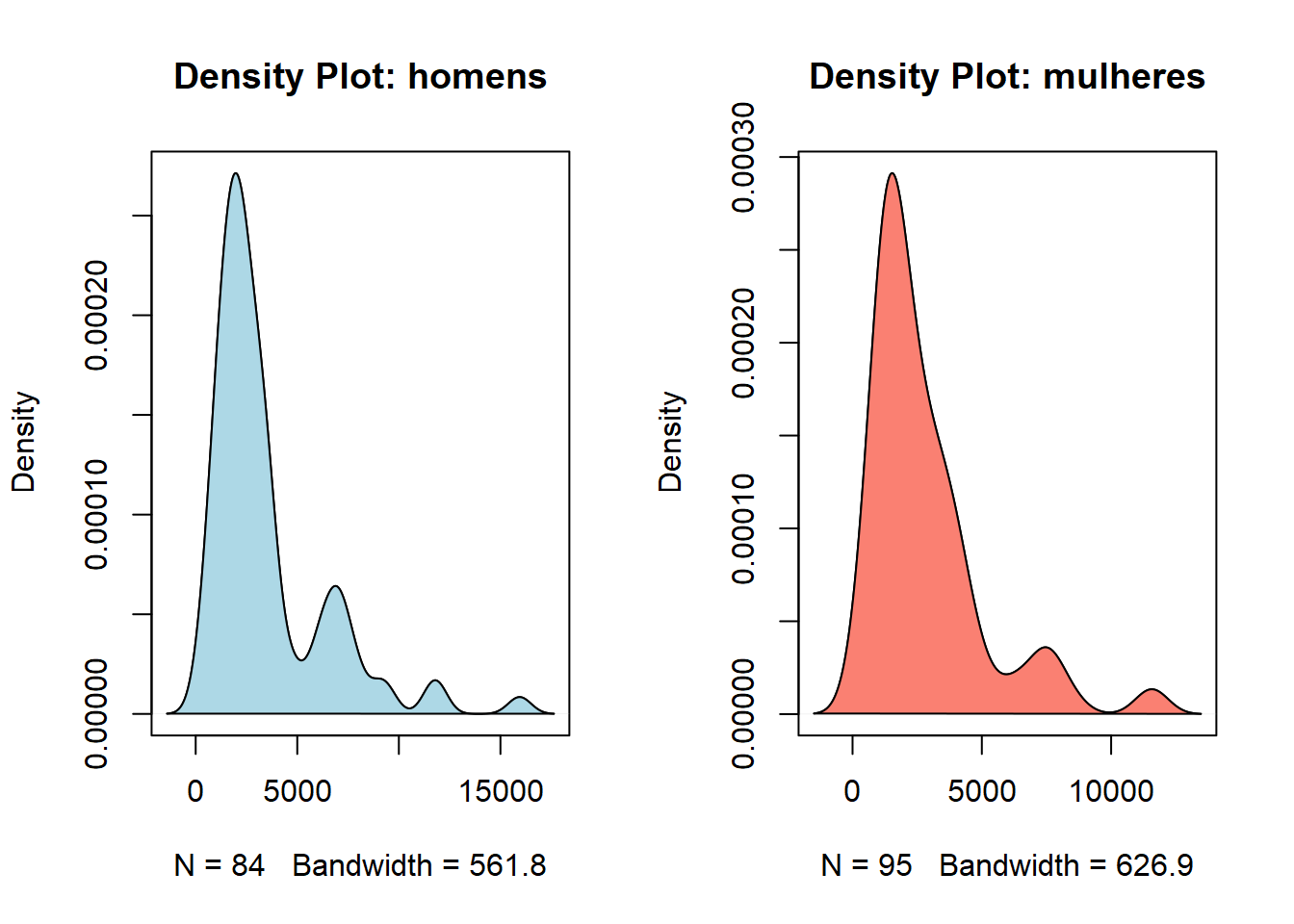

Com esse formato, a normalidade é bastante implausível e não há necessidade de realizar quaisquer testes. Para contornar esse problema, podemos tentar realizar uma transformação logarítmica:

 1# transformação logarítimica
 2log_homens = log(homens)
 3log_mulheres = log(mulheres)
 4
 5# calculando a variância após transformação
 6var(log_homens)
 7var(log_mulheres)
 8
 9# dados de densidade
10d3 = density(log_homens)
11d4 = density(log_mulheres)
12
13# separando o grid em 2 colunas
14par(mfrow = c(1,2))
15
16# visualização
17plot(d3,
18  main = "Density Plot: log(homens)")
19polygon(d3, col = "lightblue")
20
21plot(d4,
22  main = "Density Plot: log(mulheres)")
23polygon(d4, col = "salmon")

## [1] 0.5614271

## [1] 0.5229548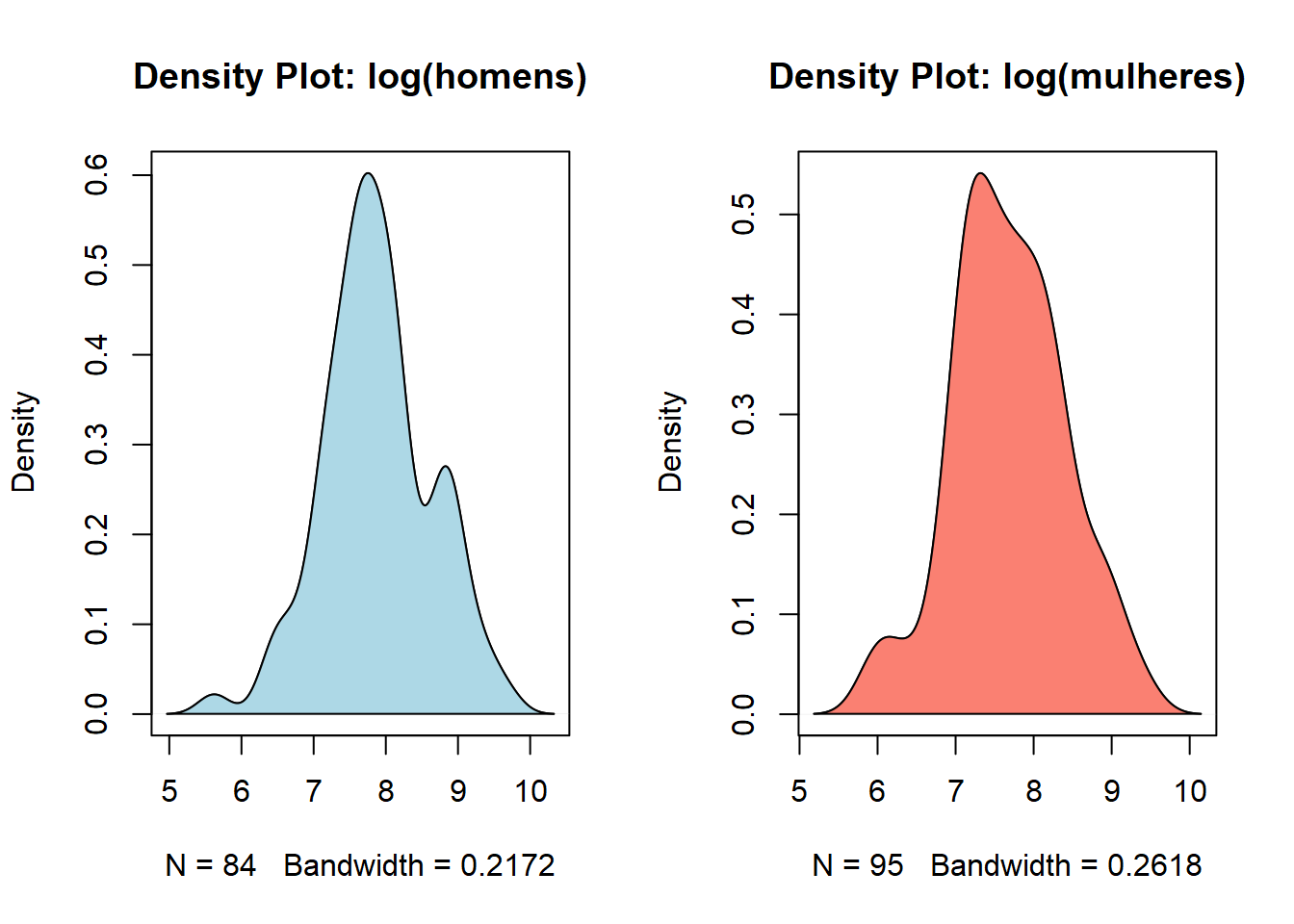

Os dados agora parecem seguir uma distribuição próxima da normal. Para verificar, pode-se realizar um teste de normalidade mas, como não é esse o tema, exploraremos o assunto em outra postagem. Por hora, vamos apenas registrar que a transformação foi exitosa e os dados agora apresentam uma distribuição próxima da normal.

1# teste de normalidade
2shapiro.test(log_homens)
3shapiro.test(log_mulheres)

## 
##  Shapiro-Wilk normality test
## 
## data:  log_homens
## W = 0.98624, p-value = 0.5147

## 
##  Shapiro-Wilk normality test
## 
## data:  log_mulheres
## W = 0.98171, p-value = 0.2071

AS HIPÓTESES

\[ \begin{cases} H_0: \sigma_1 = \sigma_2 \\ H_1: \sigma_1 \neq \sigma_2 \end{cases} \]

A hipótese nula é de que não se pode inferir, com certo nível de significância, que as variâncias são diferentes. E a hipótese alternativa é de que elas são significamente distintas.

NÍVEL DE SIGNIFICÂNCIA

\[ \alpha = 0.05 \]

Vamos utilizar um nível de significância padrão de 5%, o que quer dizer que a probabilidade de rejeitarmos a hipótese nula quando ela não deve ser rejeitada é de apenas 5%. Quanto menor for essa probabilidade, maior deve ser a diferença entre as variâncias para que possamos atestar a diferença significativa entre elas.

ESTATÍSTICA DO TESTE

\[ F = \frac{s^2_1}{s^2_2} \]

Como a estatística do teste é a razão entre as variâncias amostrais, o teste é para verificar se essa razão é diferente da unidade. Para verificarmos a estatística tabelada, precisamos de saber quantos graus de liberdade temos nas amostras:

1# graus de liberdade (n-1)
2table(data[data$Housing == "rent",]$Sex)

## 
## female   male 
##     95     84

E então a estatística tabelada será:

1# F-statistic para 95º percentil
2qf(.95, 83, 94)

## [1] 1.419123

VALOR CRÍTICO

1# calculando valor crítico
2var(log_homens) / var(log_mulheres)

## [1] 1.073567

\[ F = \frac{s^2_1}{s^2_2} = 1.07 \]

DECISÃO

Como o valor de 1.07 não excede 1.42, não podemos rejeitar a hipótese nula ao nível de 5% de significância. As variâncias não são significativamente distintas.

O TESTE F NO R

No base R, a sintaxe do teste é muito semelhante a do teste t:

1# teste F
2var.test(log_homens, log_mulheres)

## 
##  F test to compare two variances
## 
## data:  log_homens and log_mulheres
## F = 1.0736, num df = 83, denom df = 94, p-value = 0.7362
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.707196 1.638814
## sample estimates:
## ratio of variances 
##           1.073567

O sumário do teste nos diz que para que pudéssemos rejeitar a hipótese nula com $\alpha$ = 5%, a razão deveria ser na ordem de 1.64 (variância de log_homens maior do que log_mulheres) ou 0.70 (variância de log_homens menor do que log_mulheres). Alternativamente, poderíamos rejeitar a hipótese nula se aumentássemos $\alpha$ para 1-0.7362 = 26.38%, o que é uma probabilidade de incorrer no erro tipo II muito alta para ser considerada razoável.

Marcos alemães.↩︎