Atestando diferenças em médias: o teste t para amostras independentes

Suponha que você tenha duas amostras (i.e. as rendas da população negra e branca de sua cidade) e você queira comprovar que suas médias sejam significantemente diferentes, ou seja, que sejam diferentes mesmo considerando a variância e o tamanho das amostras. Isso é possível com um teste t de Student, um dos mais populares testes na estatística.

Vamos utilizar um dos datasets nativos do R para aplicar esse conceito, o mtcars. Primeiramente, vamos dar uma olhada em nossos dados.

1data = mtcars
2head(data)

##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

Uma boa forma de ilustrar o teste é verificar se as médias de consumo dos carros (mpg, miles per gallon) com 4, 6 e 8 cilindros (cyl) diferem significantemente entre si.

1# Médias amostrais
2aggregate(mpg ~ cyl, data = data, FUN = mean)

##   cyl      mpg
## 1   4 26.66364
## 2   6 19.74286
## 3   8 15.10000

Verificamos que as médias amostrais são diferentes. Resta saber se são significantemente diferentes. Plotar um boxplot pode nos ajudar a ter uma intuição. Podemos ver que, exceto pelo grupo de 4 cilindros que possui uma variância maior, os grupos são bem concentrados, de forma que podemos suspeitar que as diferenças sejam significantes.

1# Boxplot
2boxplot(mpg ~ cyl, data = data)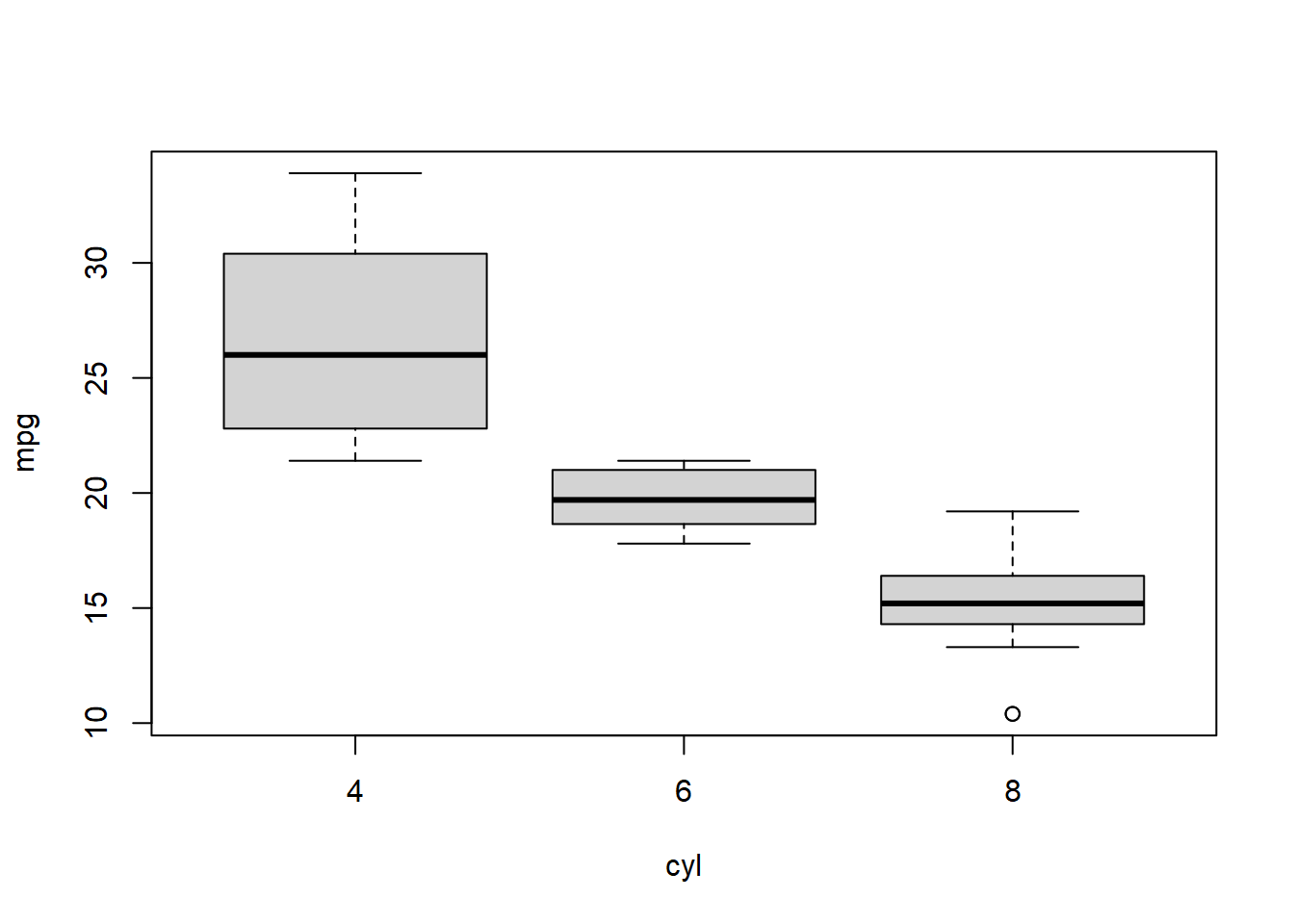

O teste t possui diversas variações — uma amostra, duas amostras pareadas, duas amostras independentes —, e correções para tratar diferenças na variância. Para este caso, temos três amostras independentes e, por hora, vamos supor que as variâncias do grupo 4 difere das demais e que a dos grupos 6 e 8 são iguais — deixaremos a análise de variâncias para outra postagem. Isso nos deixa com o teste t para duas amostras independentes.

A hipótese nula do teste é que as médias são significativamente iguais. Já a hipótese alternativa pode ser formulada como a não nulidade da diferença entre as médias ou \(\bar{X_1}\) maior ou menor que \(\bar{X_2}\). Aqui vamos usar a primeira opção:

\[ h_0: \bar{X_1} - \bar{X_2} = 0 \\ h_1: \bar{X_1} - \bar{X_2} \neq 0 \] A estatística t para esse teste é calculada da maneira abaixo. Note que se tomarmos o limite de \(t(n)\), com \(n \rightarrow \infty\), \(t\rightarrow \infty\), causando a rejeição de \(h_0\). Dessa forma, em último caso, o teste t é um teste de tamanho de amostra, ou seja, se sua amostra for suficientemente grande e as médias divergirem, elas tenderão a ser também significantemente diferentes.

\[ t = \frac{\bar{X_1} - \bar{X_2}}{s_p . \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \]

Como primeiro caso, vamos comparar as médias de consumo dos veículos com 6 e 8 cilindros. Como estamos considerando que suas variâncias são iguais, temos de usar o argumento var.equal = TRUE:

1# teste t para 6 e 8 cilindros
2t.test(mpg ~ cyl, data = data[which(data$cyl != 4),], var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  mpg by cyl
## t = 4.419, df = 19, p-value = 0.0002947
## alternative hypothesis: true difference in means between group 6 and group 8 is not equal to 0
## 95 percent confidence interval:
##  2.443809 6.841905
## sample estimates:
## mean in group 6 mean in group 8 
##        19.74286        15.10000

Com p-valor de zero, podemos rejeitar a hipótese nula e considerar que as médias de consumo entre os veículos de 6 e 8 cilindros diferem.

Para as demais comparações, vamos usar o default para var.equal que é FALSE. Isso significa aplicar a correção de Welch para amostras independentes e de variância diferentes. Como esperado, também podemos rejeitar a hipótese nula e confirmar a diferença nas médias de consumo entre os veículos de 4 e 6 cilindros e 4 e 8 cilindros.

1# teste t para 4 e 8 cilindros
2t.test(mpg ~ cyl, data = data[which(data$cyl != 6),])
3
4# teste t para 4 e 6 cilindros
5t.test(mpg ~ cyl, data = data[which(data$cyl != 8),])

## 
##  Welch Two Sample t-test
## 
## data:  mpg by cyl
## t = 7.5967, df = 14.967, p-value = 1.641e-06
## alternative hypothesis: true difference in means between group 4 and group 8 is not equal to 0
## 95 percent confidence interval:
##   8.318518 14.808755
## sample estimates:
## mean in group 4 mean in group 8 
##        26.66364        15.10000

## 
##  Welch Two Sample t-test
## 
## data:  mpg by cyl
## t = 4.7191, df = 12.956, p-value = 0.0004048
## alternative hypothesis: true difference in means between group 4 and group 6 is not equal to 0
## 95 percent confidence interval:
##   3.751376 10.090182
## sample estimates:
## mean in group 4 mean in group 6 
##        26.66364        19.74286

Easy peasy lemon squeezy, não é?